
3. فرکتال
3-1.الگوی فرکتالواژة فرکتال مشتق از واژة لاتینی فراکتوس- به معنی سنگی که به شکل نامنظم شکسته خرد شده است- در سال ۱۹۷۵ برای اولین بار توسط بنوت مندل بروت مطرح شد. فرکتال ها، شکل هایی هستند که بر خلاف شکل های هندسی اقلیدسی، به هیچ وجه منظم نیستند. با ملاحظه اشکال موجود در طبیعت، مشخّص می شود که هندسة اقلیدسی قادر به تبیین و تشریح اشکال پیچیده و ظاهراً بی نظم طبیعی نیست (قبادیان، 1382 : 167 – 166). اصول رياضي هندسه طبیعت یا هندسه فركتال و توصيف بسياري از اشياي فركتال به گذشتة دوري بر ميگردد (شمس، 1380 : 50).
این هندسه سال هاست که توسط معماران و ریاضی دانان متعدّدی مورد بحث و بررسی قرارگرفته و به کارگیری آن در معماری و هندسه مصنوع مورد شک و تردید، نقض یا دفاع واقع شده است (افتخارزاده، 1384 : 100)..نظريّة فركتال برای توصيف پيچيدگي در اشكال به كار ميرود (پناهي، مختاباد امرئي، كريمي خياوي، 1388 : 61 ). فرکتال ها شکل هایی هستند که برعکس شکل های هندسة اقلیدسی، به هیچ وجه به معنی متعارف، منظم نیستند.
این شکل ها اولاً سراسر نامنظم اند، ثانیاً میزان بی نظمی آن ها در همة مقیاس ها یکسان است، یعنی به نوعی دیگر منظم اند. جسم فرکتالی از دور و نزدیک یکسان دیده می شود (خاک زند، احمدی، 1386 : 35-47). اشكال فركتال با فرآيندهاي پويا توليد مي شوند. فرآيندهاي پويا، فرآيندهايي هستند كه داراي حافظه هستند و رفتار آن ها به گذشته بستگي دارد. الگوی فرکتال می تواند فضای ایجاد شده توسط ساختار متفاوت فرکتال را اشغال نماید و الگوی پیچیده تری را حاصل کند. چنین نمونه ای در طبیعت متداول تر است و کمک بسیار زیادی در توضیح تنوع ها و زیبایی های موجود در محیط طبیعی میکند (بل، 1382 : 33).
3-2. بررسی ویژگی های فرکتال ها
در فرکتالها، اجزا و عناصر، در مقیاسهای مختلف تکرار می شوند. هر شکل از قطعات کوچکتری تشکیل شده است که این قطعات با شکل اولیه متشابه هستند؛ به عبارت دیگر وقتی که یکی از قطعات کوچک تشکیل دهنده را به مقیاس شکل اصلی می رسانیم، دقیقاً همان شکل به دست می آید. این ویژگی را خودمتشابهی می نامیم.
فرکتالها به وسیله فرایندی تکرارشونده شکل می گیرند و هر تکرار از نتیجة قبلی اش ساخته شده است. این ویژگی را تکرارشوندگی می نامیم. •فرکتالها در هر مقیاسی یکسان به نظر می رسند. مجموعه هاي فركتال از زيرمجموعه هايي تشيكل شده اند كه اين زيرمجموعه ها شامل مجموعه هاي بزرگتر هستند. مجدداً اين مجموعه ها از زيرمجموعه هاي كوچكتري تشيكل شده اند. اين زير مجموعه ها نيز شبيه مجموعه هاي بزرگتر هستند که این ویژگی را خردمقیاسی می نامیم.
0فرکتال ها ابعاد منحصربه فردی دارند که به صورت ریاضی تعریف شده اند.. بُعد فرکتال یک معیار ریاضی در تعیین درجة پیچیدگی بافت در حال نمایش است که این ویژگی را بعد اعشار می نامیم(Davis,2008;2 Pellonisz). با نزدیک شدن به جسم فراکتال، میبینیم که تکه های کوچکی از آن که از دور همچون دانه های بی شکلی به نظر می رسید، به صورت جسم مشخّص در می آید که شکلش کم و بیش مانند همان شکلی است که از دور دیده می شود. در طبیعت نمونه های فراوانی از فراکتال ها دیده می شود.
درختان، ابرها، کوه ها، رودها، لبة سواحل دریا و گل کلم ها اجسام فراکتال هستند. در واقع، بخش کوچکی از درخت که شاخه آن باشد، شباهت به کل درخت دارد. این مثال را می توان در مورد ابرها، گل کلم، صاعقه و سایر اجسام فرکتال عنوان نمود. چند نمونه از فرکتال ها در جدول شمارة 6 آورده شده است.
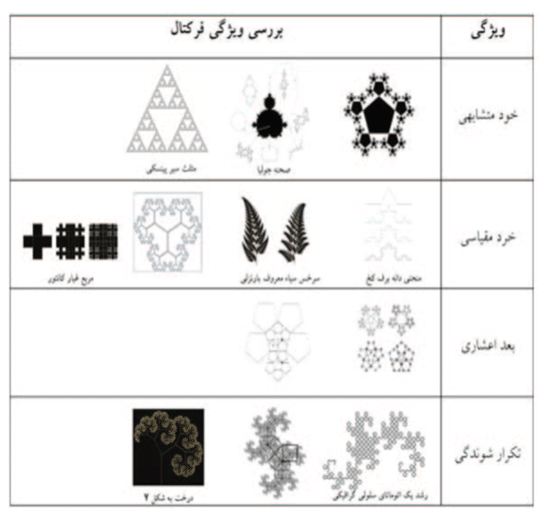
جدول 6. دسته بندی ویژگی های فرکتال ها
همان طور که در جدول شمارة 6، مشاهده می شود به طور نمونه دانة برفي کخ ( Kock ) در همه جا پيوسته است، امّا در هيچ جا مشتق پذير نيست. اين منحني داراي محيط بي نهايت با سطح محدود است. نكتة قابل توجّه اين دانة برفي با استفاده از فرآيندی تكراري و پويا توليد شده است، درصورتي كه اشيای اقليدسي با استفاده از فرآيندهاي ايستا توليد مي شوند. مثلث سرپینسکی (Serpinski ) نیز جزء يكي از معروف ترين اشيای فركتال است. این مثلث متساوی الاضلاع خاصيّت خودمتشابهی دارد (قبادیان، Davis,2008;2-9 166-167 :1382).
4. بررسی مقایسة ویژگی گره ها و فرکتال ها
در جدول شمارة 7، چند نمونه از گره و فرکتال را در کنار هم برای نمایش ویژگی های مشترک آورده ایم. با توجّه به نتایج به دست آمده از بررسی هایی که در ویژگی های گره ها انجام دادیم، به نتایجی دست یافتیم که مهم ترین آن این است:گره ها و فرکتال ها فصلنامه ویژگی های مشترکی دارند که هم در «طبیعت » یافت می شوند و هم از اشکال موجود در طبیعت بهره گرفت هاند؛ به عبارت دیگر هر دو منشأ طبیعی دارند.
نتیجه گیری
این نکته حائز اهمیّت است که همة تحلیل ها و نمایش ویژگی گره ها که در این مقاله بررسی گردیده، توسط برنامه های رایانه ای و با صرف وقت و دقت صورت گرفته است. حال این که هنرمندان اسلامی با چه ذوق هنری، درایت و دقّت بالایی از زما نهای دور با ابزار دستی و ساده، چنین نقوش متوازن، زیبا، هنرمندانه و پر رمز و رازی را خلق کرده اند، جای بسی تأمل و تفکر دارد. شیوة هنروری این هنرمندان، محققان را در سراسر جهان شیفته خود کرده است.
بررسی گره ها به روشنی نشان داد که هندسۀ گره ها، ویژگی های لازم را برای قیاس با هندسۀ فرکتال دارد. ویژگی های مشترک فرکتال ها و گره ها را در جدول جمع بندی میبینیم. در این مقاله، فرکتال ها با چهار ویژگی اصلی که با آن شناخته می شوند، با گره ها مقایسه شده اند. گره ها علاوه بر ویژگی های فرکتالی، ویژگی دیگری نیز دارند که آن ها را در جدول شمارة 8 می بینیم. حال آن که ممکن است فرکتال ها این ویژگی ها را نیز داشته باشند که بررسی آن ها در این مقاله نمی گنجد.
گره ها دارای ویژگی های تقارن، دوران، تناسب، نوزایی، مرکزگرایی، چند لایه ای (فولد)، مفهو مگرایی و نمادگرایی هستند. فرکتال ها دارای اشکال هندسه نااقلیدسی، هندسه غیر خطی، بی نظمی، اشکال غیرمتعارف، قوانین خاص، بی انتهایی و اشکال پیچ درپیچ هستند. هر دو دارای ویژگی های مشترک خود متشابهی، خرد مقیاسی، بعد اعشار و تکرارشوندگی هستند.
طبیعت، دستاورد بهترین معمار یعنی خدا و بهترین سرچشمة الهام انسان است.گره ها و فرکتال ها از اشکال موجود در طبیعت بهره و از آن الگو گرفته اند(هر دو منشأ طبیعی دارند). از آن جایی که در طبیعت تعادل وجود دارد، اشکال گره ها مانند فرکتال ها دارای تعادل هستند. برای وضوح مطلب نتایج را می توان در قالب دیاگرام زیر نشان داد:
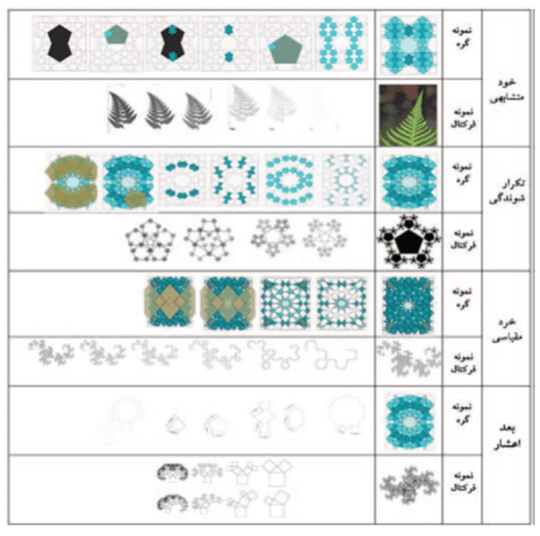
جدول شمار ة 7 : مقایسه گره ها و فرکتال ها از دیدگاه ویژگی های مشترک


جدول شمار ة 8 : ویژگی های گره ها و فرکتال ها

نتیجه آن که:
- هنرمندان اسلامی به مفهوم هندسه ای که از فرم های طبیعی گرفته شده بود، واقف بوده اند. این هندسه بعدها به نام هندسه فرکتال شناخته شد.
- اجزای تشکیل دهندۀ هندسۀ گره ها، ویژگی های هندسۀ فرکتال ها را دارند؛ از جمله: خودمتشابهی، خُرد مقیاسی، بُعد اعشار و تکرار شوندگی(جدول شمارة 8 ).
- گره ها علاوه بر ویژگی های فرکتالی، دارای ویژگی های دیگری مانند تقارن، دوران، مرکزگرایی، تناسب، چندلایگی و نوزایی هستند (جدول شمارة 8 ).
- طبیعت، دستاورد بهترین معمار یعنی خدا و بهترین سرچشمه الهام انسان است. گره ها و فرکتال ها از اشکال موجود در طبیعت بهره و از آن الگو گرفته اند (هر دو منشأ طبیعی دارند.) هردو ویژگی های مشترکی دارند که هم در «طبیعت » یافت می شوند و هم از اَشکال موجود در طبیعت بهره گرفته اند. در طبیعت تعادل وجود دارد وگره ها نیز مانند فرکتال ها دارای تعادل هستند.
- در پس اشکال بدیع و پیچیده گره ها علاوه بر ویژگی های نام برده شده، مفاهیم و ویژگی های دیگری مانند «مفهوم گرایی » و «نمادگرایی» و «فولد یا چندلایه ای » نیز وجود دارد که نیازمند بررسی بیش تری است.
پی نوشت ها
- . فرهنگستان علوم واژه “برخال”را معادل “فرکتال” انتخاب نموده است.”برخ” و “برخه”به معنای کسر، جزئی از کل و پاره است. واژه “برخی” به معنای “پاره ای” در فارسی امروز از همین ریشه است و پسوند “ال” به معنای نسبت و شباهت است (انصاری آملی).
- Roger Penrose ریاضی دان و کیهان شناس انگلیسی Durham,1971
- Peter Lu دکتر،محقق در دانشکده فیزکی و دانشکده مهندسی و علوم کاربردی در دانشگاه هاروارد ماساچوست است. او به خاطر کشف خود در مورد گره و الگوهای شبه کریستالی درمعماری اسلامی شناخته شده است.
- Paul Steihaurdt
- Keite kritchlu مدرس، نویسنده و استاد معماری در انگلستان و از بنیان گذاران آکادمی Temenos است.
- Gulru Nacipoglu
- Craig S. Kaplan دکتر فلسفه از دانشگاه واشنگتن وی الگوهای تزیین های اسلامی را به دو دسته گل شکل و ستاره ای شکل تقسیم بندی نموده و به نحوة ترسیم الگوها با نرم افزار های گرافیکی پرداخته است. Kaplan, Craig S 2002
- Frode Ronning به بررسی الگوهای اسلامی و گروه های تقارن پرداخته است.
- Henry Richard دوره های عملی هندسه از الگوهای اسلامی را در موزه بریتانیا در لندن تدریس می کند.
- رضا سرهنگی دکترای ریاضیات کاربردی (نظریه کنترل سیستم های پارامتر توزیع شده) از دانشگاه ویچیتا، کانزاس است. وی علاوه بر تدریس دروس ریاضیات و هنر، آشفتگی و فرکتال و ارتباط ریاضیات با علوم را نیز در دانشکده کالج تدریس می کند و به بررسی تزیین های انجام شده بر روی گنبدها پرداخته است .
- فرهنگ معین، مدخل آ.
- ستاره پنج پر یا پنتاگرام، شکلی هندسی است که از پنج خط تشکیل شده و به شکل ستاره است (www.wikipedia.org)
- Decagram (Shamsa)
- کایت و دارت بخش های تشکیل دهندة چیدمان پریودی پنرز هستند که با مجموعه ای مرحله ای و از اشکال ریزتر با تکرار از طرح اصلی به وجود می آید.
- کایت:چهارضلعی است که چهار گوشه آن دارای زاویه های 72 ، 72 ، 72 و 144درجه است. کایت ممکن است نیم ساز دو محور تقارن خود را رسم کرده و دو زاویه حاد، برای شکل دادن مثلث رابینسون به وجود آورد.
- دارت: چهارضلعی غیر محدبی است که زوایه های داخلی اش 36 ، 36 و 216 درجه است. دارت ممکن است نیم ساز دو محور تقارن خود را رسم کرده و دو زاو ةی منفرجه، برای شکل دادن مثلث رابینسون به وجود آورد.
- روکاری، معمولاً هنری ایرانی برای تزیین قسمت های داخلی گنبد است که در بسیاری از موارد با هنر موزایی ککاری، سرامی ککاری و آیینه کاری همراه است.
- self-similar
- formed by a repetitive process in which each repetition builds on the prior resu
- look the same at any scale
- unique dimensions (roughness)
- پیدایش شکل های نو در گره ها حاصل تحلیل آن ها )نگارندگان(.
- ویژگی های نهفته در آلت گره ها که همواره در ظاهر آن نمایان نیست و مفهومی عرفانی و گاه فلسفی و در واقع فراتر از شکل مادی و صوری آن ها دارد )نگارندگان(.
- ویژگی های ظاهری و مادی که یا در ظاهر آلت گره ها نمایان است و یا نشانگر و یادآور مفهومی خاص است (نگارندگان)؛ مثلاً دایره نماد آسمان و مربع نماد زمین است، در حالی که دارای مفاهیم عرفانی بسیاری نیز هستند. در دایره مفاهیمی از قبیل کشش، پایداری و ناپایداری و ... و در مربع مفاهیم ایستایی، ثبات و برابری نهفته است.
- چند لایه ای یا فولد يعني چين و لايه. لايه هاي هزارتو، هر لايه در كنار لايه ديگر، همه چيز در كنار هم است. همه چيز افقي است.( قباديان، 1382 : 152 ).
فهرست منابع و مراجع
- افتخار زاده، ساناز، (1384)، «هندسه طبیعت در برابر هندسه اقلیدسی» ، فصلنامه معماری و ساختمان، شماره ۸.
- انصاری آملی، عبدالرضا، مبانی ریاضی هندسه فرکتال ها، انتشارات فضا.
- امیر غیاثوند، محبوبه،(1382) ، هنر گره چینی در معماری، موسسه فرهنگی تکوک زرین، چاپ اول.
- بلخاری قهی، حسن، (1384) مبانی عرفانی هنر و معماری اسلامی(کیمیای خیال)، نشر سوره مهر.
- بل، سایمون(،1382) ، منظر: الگو، درک و فرآیند، ترجمه بهناز امین زاده، تهران، دانشگاه تهران.
- بلوکباشی، علی، (1383) ، « آرمانگرایی در معماری تزیینی ایران »، مجموعه مقالات، دومین کنگره معماری و شهرسازی ایرانی، ارگ بم-کرمان جلد 5.
- بورکهارت، تيتوس،( 1376)، ارزش های جاويدان هنر اسلامی، ترجمه سيد حسين نصر، در مبانی هنر معنوی، تهران، دفتر حوزه هنری سازمان تبليغات اسلامی.
- بورگوان، ج،(1362) ، طرحهای اسلامی(هندسی) هنر گره سازی، کارگاه هنر.
- بویل، کارل، هندسه فرکتال در معماری و طرّاحی، ترجمه محمد اشرف گنجویی، حسین فلاح، انتشارات دانشکاه کرمان.
- خاک زند، مهدی و امیراحمد احمدی، (1386)، « نگاهی اجمالی به رویکرد میان طبیعت و معماری »، باغ نظر، سال چهارم، پاییز و زمستان.
- حجازی، مهرداد،(،1384)،« هندسه مقدس در طبیعت و معماری ایرانی »، مجله بنا.
- خوارزمی، ابوریحان محمد بن احمد،(1326) ، کتاب التفهیم، جلال الدین همائی، انتشارات انجمن آثار ملی، تهران.
- دکزی، گیورگی، (1388) ، ناکرانمندی کرانمند، ترجمه حمیدرضا کرمی، پرچین، تهران.
- دهقان نژاد، اکبر،(1383)، پژوهشی در روش های ریاضی موجود برای بررسی نقوش هندسی و جایگاه آن در هنر کاشیکاری اسلامی و ایرانی، «مجموعه مقالات دومین کنگره تاریخ معماری و شهرسازی ایرانی، ارگ بم - کرمان، جلد پنجم.
- رئیس زاده، مهناز و حسین مفید،(1383) ، احیای هنرهای از یادرفته )مبانی معماری سنتی در ایران به روایت استاد حسین لرزاده(، انتشارات مولی، تهران.
- زمرشیدی، حسین، (1365)، گره چینی در معماری اسلامی و هنرهای دستی، مرکز نشر دانشگاهی، تهران.
- سامانیان، صمد، (1387) ، هندسه نقوش اسلامی، آموزش های فنی و حرفه ای رسمی، مؤسسه فرهنگی هنری شقایق روستا، چاپ اول، تهران.
- شمس، حسن،( 1380) ، شهر هوشمند، پايان نامه فوق ليسانس، دانشگاه علم و صنعت، تهران.
- صبا، منتخب،(1383) ، نقوش هندسی اسلامی )طرح و رسم(، نور حکمت، مشهد.
- صفا، ذبیح اله،(1365)، تاریخ علوم عقلی در تمدن اسلامی، تا اواسط قرن پنجم، ج ١، امیرکبیر، تهران.
- فارابی، ابونصر محمدبن محمد، (1364) ، احصاء العلوم، ترجمه حسین خدیو جم، انتشارات علمی و فرهنگی، تهران.
- . فلامکی، منصور، (1381) ، ريشه ها و گرايش های نظری معماری، نشر فضا، مؤسسه علمی و فرهنگی فضا، تهران.
- قبادیان، وحید، (1382) ، مبانی و مفاهیم در معماری معاصر غرب، چاپ اول، انتشارات دفتر پژوهشهاي فرهنگي، تهران.
- کیانمهر، قباد و محمد خزایی، (1385) ، مفاهیم و بیان عددی در هنرگره چینی صفوی، کتاب ماه هنر، فروردین و اردیبهشت.
- محمودی نژاد، هادی، (1388) ، معماری زیست مبنا، طحان، تهران.
- مددپور، محمد،(1374) ، تجلیات حکمت معنوی در هنر اسلامی، امیر کبیر، تهران.
- نجیب اوغلو، گل رو،(1380) ، هندسه و تزیین در معماری اسلامی، ترجمه مهرداد قیومی بیدهندی، انتشارات روزبه، تهران.
- نصر، سید حسین، (1366) ، علم در اسلام ، ترجمه احمد آرام، سروش ، تهران.
- نصر، سید حسین، (1375) ، هنر و معنویت اسلامی، ترجمه رحیم قاسمیان، دفتر مطالعات دینی هنر، تهران.
- نوایی، کامبیز،( 1383) ، نکاتی پیرامون نقوش اسلامی، کنگره تاریخ معماری و شهرسازی، جلد دوم.
- Aljamali .Ahmad M, and Ebad Banissi (2003), Grid Method Classification of Islamic,Geometric Patterns, WSCG , February, 3-7Plzen, Czech Republic.
- Davis, Betsey (2008), Integration of Fractal Geometry into Mathematics and Science Curricula, MathScience Innovation Center.
- Fischbein, E (1987), Intuition in science and mathematics. An educational approach. Dordrecht, Kluwer.
- Henry, Richard, (2007), Pattern, Cognition and Contemplation: Exploring the Geometric ,Art of Iran, Public lecture at the Middle East Association on 27 April. Published in the Journal of the Iran Society.
- Kaplan, Craig S, (2002), Computer Graphics and Geometric Ornamental Design, a dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy, University of Washington.
- Lu, Peter J. Steinhardt, Paul J, (2007), Decagonal and Quasicrystalline Tilings in Medieval Islamic Architecture, Science 315, 1106.
- Pellonisz, A.J., Neural Geometry:Towards a Fractal Model of Neurons, New York University Medical Center.
- Penrose, R (1989),Aperiodicity and Order (ed. Jaric, M. V.), vol. 2.
- Ronning, Frode, Islamic patterns and symettry group.
- Sarhangi, Reza, (1999), The Sky Within: Mathematical Aesthetics of Persian Dome Interiors, Nexus Network Journal - Volume I, 1999.
- www.patterninislamicart.com, www.tilingsearch.org
- www.peterlu.org
- www.newsweek.com
- www.library.thinkquest.org/3493/frames/fractal
- www.classes.yale.edu/fractals/panorama
- www.miqel.com
- www.mathworld.wolfram.com
